Séquence Parallélogramme Samedi 21 décembre 2024
Faire Comprendre

Séance n°9 : Constructions de parallélogrammes sur l'écran d'ordinateur
Séquence

Séquence

Séquence
    - Séance n°0
    - Séance n°1
    - Séance n°2
    - Séance n°3
    - Séance n°4
    - Séance n°5
    - Séance n°6
    - Séance n°7
    - Séance n°8
    -  Séance n°9
    - Séance n°10
    - Séance n°11

Séquence

Il s'agit dans cette séance de chercher différentes constructions du parallélogramme.





   
Impression séance     Impression séance et commentaires.

Constructions de parallélogrammes sur l'écran d'ordinateur: Commentaires déroulement

Nous donnons ci-dessous les programmes correspondant à des constructions possibles. (Les lettres ne sont employées ici que pour faciliter la communication, elles ne seront pas employées par les élèves.)

- Construction utilisant p1 et p2, la plus facile ici.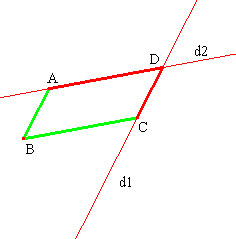


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

segment [A B]
segment [B C]
d1 : droite passant par A et parallèle au segment [B C] (invisible)
d2 : droite passant par C et parallèle au segment [A B] (invisible)
D : intersection des 2 droites d2 et d1
segment [A D]
segment [D C]

Néanmoins, les élèves peuvent continuer à réaliser le parallélisme avec une double perpendicularité (réinvestissement de la séance précédente).

- Construction utilisant p1 et l1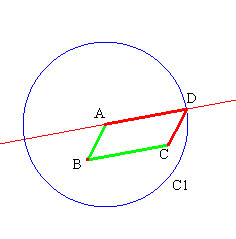


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

segment [A B]
segment [B C]
d1 : droite passant par A et parallèle au segment [B C] (invisible)
C1 : compas (centre A, rayon [B C])
D : intersection du cercle C1 et de la droite d1 (choix du point du même côté que C / [A B])
segment [A D]
segment [D C]

La construction utilisant p1 et l2 n'assure que la présence d'un trapèze isocèle, qui dans certains cas peut être un parallélogramme…

- Construction utilisant l1 et l2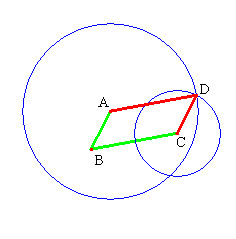


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

segment [A B]
segment [B C]
C1 : compas (centre A, rayon [B C])
C2 : compas (centre C, rayon [A B])
D : intersection des deux cercles C1 et C2 (autre que B)
segment [A D]
segment [D C]

- Construction utilisant m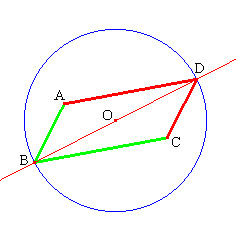


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

segment [A B]
segment [B C]
O milieu de [A C]
d1 : droite passant par B et O
C1 : cercle (centre O passant par B)
D : intersection de d1 et C1
segment [A D]
segment [D C]


Fermer

Constructions de parallélogrammes sur l'écran d'ordinateur: Commentaires matériel

Le menu "para2.men" se présente comme suit :


Fermer

Constructions de parallélogrammes sur l'écran d'ordinateur: Commentaires objectifs

Le changement d'instruments change la nature des difficultés :
- la construction de droites parallèles ne pose plus que le problème d'une bonne utilisation de la commande ;
- l'utilisation de "Compas" pour l'isométrie et la création des segments sur les droites supports peuvent encore créer des problèmes ;
- la construction par les diagonales est complexe puisque, après la construction du milieu d'un diagonale, il faut tracer une droite (et non un segment) passant par ce milieu et penser à utiliser un cercle centré en ce milieu pour avoir l'autre diagonale.

Les constructions ne sont pas toutes exigibles de tous les élèves.
Fermer

Constructions de parallélogrammes sur l'écran d'ordinateur: Déroulement

- Phase 1 / collectif / Présentation de la tâche
Ouvrir ou faire ouvrir le logiciel et le fichier "para2.men".
Réafficher les propriétés du parallélogramme trouvées dans la séance 4 avec leurs abréviations.

Avec les commandes dont vous disposez, vous allez chercher le maximum de constructions différentes d'un parallélogramme (utilisant des propriétés différentes) à partir de deux segments ayant une extrémité commune.
Vérifiez vos constructions en déplaçant les points attrapables.
Lorsqu'elles sont correctes sauvegardez-les et notez sur une feuille le nom de votre fichier et les propriétés utilisées

- Phase 2 / groupes de 2 / constructions

- Phase 3 / collectif / correction
Se servir du vidéo-projecteur et faire exécuter les constructions par différents élèves.
On retrouvera tout ou partie des constructions vues en séance 5 et rappelées dans les commentaires du déroulement. L'enseignant peut noter (ou regarder simplement) les productions des élèves.


Fermer

Constructions de parallélogrammes sur l'écran d'ordinateur: Fichiers annexes

Liste des fichiers liés à cette séance

  • "sean_para2.men" : Menu simplifié dans Cabri

    • Fermer

    Constructions de parallélogrammes sur l'écran d'ordinateur: Matériel

    Matériel nécessaire pour chaque groupe d'élèves :

    • un ordinateur avec le menu simplifié "para2.men"
    • la fiche des commandes Cabri

    Matériel nécessaire pour l'enseignant

    • si possible un vidéoprojecteur pour corriger.


    Fermer

    Constructions de parallélogrammes sur l'écran d'ordinateur: Objectifs

    Objectif général : faire construire un parallélogramme dans l'espace instrumenté par le logiciel de géométrie dynamique.

    Dans cette séance,
    - reprendre les constructions vues dans la séance 5
    - associer constructions du parallélogramme et propriétés utilisées
    - utiliser à bon escient les commandes du logiciel
    Fermer
    2024 MAGESI - C.Rolet