Séquence Parallélogramme Jeudi 18 avril 2024
Faire Comprendre

Séance n°10 : Synthèse sur les quadrilatères
Séquence

Séquence

Séquence
    - Séance n°0
    - Séance n°1
    - Séance n°2
    - Séance n°3
    - Séance n°4
    - Séance n°5
    - Séance n°6
    - Séance n°7
    - Séance n°8
    - Séance n°9
    -  Séance n°10
    - Séance n°11

Séquence

Il s'agit dans cette séance de faire une synthèse sur les propriétés des quadrilatères particuliers.





   
Impression séance     Impression séance et commentaires.

Synthèse sur les quadrilatères: Commentaires déroulement

La séance est composée de 4 moments, les trois premiers ayant la même structure. On peut l'annoncer aux élèves afin qu’ils aient une certaine autonomie et une plus grande efficacité dans leur travail.

Insister pour qu'il y ait un essai de réflexion sur les points que l'on peut déplacer.

Nous donnons ci-dessous les réponses pour le statut des points.

Parallélogramme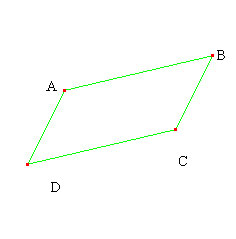


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

A, D et C sont des points libres (déplaçables avec deux degrés de liberté) ;
B est construit (entraînable) comme point d'intersection de la parallèle à (AD) passant par C et de la parallèle à (DC) passant par A

Losange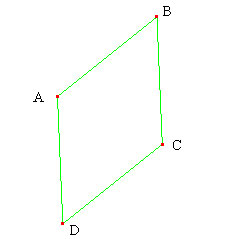


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

A et C sont des points libres ;
B se déplace sur la médiatrice de [AC] ;
D est construit comme point d'intersection du cercle de centre O passant par B ave la droite (OD).

Rectangle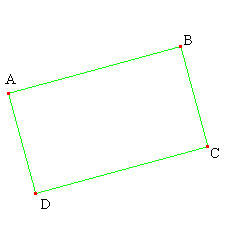


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

A et B sont des points libres ;
D se déplace sur la perpendiculaire à [AB] en A
C est construit comme point d'intersection de la perpendiculaire à [AB] passant par B avec la perpendiculaire à [AD] passant par D.

Carré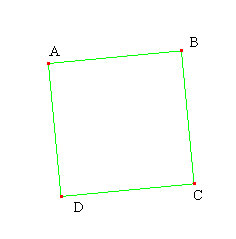


Cliquez sur l'image pour ouvrir l'applet et déplacer les objets.

A et B sont des points libres ;
C et D sont des points construits.


Fermer

Synthèse sur les quadrilatères: Commentaires matériel

On aura intérêt à mettre les fichiers utilisés dans un même dossier et les rendre ainsi faciles à ouvrir par les élèves.

Le tableau peut être photocopié à raison de 2 par page.
Fermer

Synthèse sur les quadrilatères: Commentaires objectifs

Les propriétés des quadrilatères particuliers, très classiques, sont celles énoncées dans le tableau distribué aux élèves. Le relevé de ces propriétés se fait grâce au déplacement des points libres.
Le dynamisme du logiciel est particulièrement pertinent pour "montrer" la hiérarchie des quadrilatères : en déplaçant des sommets du parallélogramme, on peut obtenir à l'écran chacun des autres quadrilatères particuliers ; etc.
La réflexion sur le statut des points est ébauchée par les élèves : certains élèves peuvent déjà percevoir que les points n'ont pas tous le même statut et que "plus le quadrilatère a de propriétés, moins on peut bouger les points". Les précisions données dans les synthèses ne seront pas données spontanément...


Fermer

Synthèse sur les quadrilatères: Déroulement

- Phase 1 / collectif / donnée de la consigne
Prévenir les élèves de l'ensemble du déroulement de la séance en trois temps.
Distribuer la feuille polycopiée avec le tableau récapitulatif.
Faire ouvrir le fichier "parallelogramme.fig" et indiquer qu'un clic prolongé de la souris signale les points que l'on peut attraper.

Quels sont les points que vous pouvez attraper et déplacer? pourquoi?
Notez dans la première colonne du tableau les propriétés sur les diagonales et les côtés qui restent vérifiées dans les déplacements.
Montrez, en déplaçant les points attrapables, qu'à partir du parallélogramme on peut obtenir un losange, un rectangle, un carré.

- Phase 2 / groupes de 2 / exécution de la tâche

- Phase 3 / collectif / synthèse sur le parallélogramme
Se servir du vidéoprojecteur et faire exécuter les déplacements par différents élèves. Vérifier la justesse des propriétés dans la première colonne du tableau.

Dans un cabri-parallélogramme, trois sommets sont attrapables et déplaçables librement, le quatrième est seulement entraînable par les autres.
Un losange est un parallélogramme particulier (ou dans l'ensemble des parallélogrammes il y a les losanges).
Un rectangle est un parallélogramme particulier (ou dans l'ensemble des parallélogrammes il y a les rectangles).
Un carré est un parallélogramme particulier (ou dans l'ensemble des parallélogrammes il y a les carrés).

- Phase 4 / collectif / donnée de la consigne
Faire ouvrir le fichier "losange.fig".

Quels sont les points que vous pouvez attraper et déplacer? pourquoi? Notez dans la deuxième colonne les propriétés sur les diagonales et les côtés qui restent vérifiées dans les déplacements. Montrez, en déplaçant les points, qu'à partir du losange on peut obtenir un carré.

- Phase 5 / groupes de 2 / réalisation de la tâche

- Phase 6 / collectif / synthèse sur le losange
Se servir du vidéoprojecteur et faire exécuter les déplacements par différents élèves. Vérifier la justesse des propriétés dans la deuxième colonne du tableau.

Dans un cabri-losange deux sommets sont attrapables et déplaçables librement, un sommet est attrapable et se déplace sur un objet, un sommet est seulement entraînable.
Un carré est un losange particulier (ou dans l'ensemble des losanges il y a les carrés).

- Phase 7 / collectif / donnée de la consigne
Faire ouvrir le fichier "rectangle.fig".

Quels sont les points que vous pouvez attraper et déplacer ? pourquoi ? Notez dans la troisième colonne les propriétés sur les diagonales et les côtés qui restent vérifiées dans les déplacements. Montrez, en déplaçant les points, qu'à partir du rectangle on peut obtenir un carré.

- Phase 8 / groupes de 2 / réalisation de la tâche

- Phase 9 / collectif / synthèse sur le rectangle
Se servir du vidéoprojecteur et faire exécuter les déplacements par différents élèves. Vérifier la justesse des propriétés dans la troisième colonne du tableau.

Dans un cabri-rectangle deux sommets sont attrapables et déplaçables librement, un sommet est attrapable et se déplace sur un objet, un sommet est seulement entraînable.
Un carré est un rectangle particulier (ou dans l'ensemble des rectangles, il y a les carrés).

- Phase 10 / collective / donnée de la consigne
Faire ouvrir le fichier "carre.fig".

Quels sont les points que vous pouvez attraper et déplacer ? pourquoi ? Notez dans la quatrième colonne les propriétés sur les diagonales et les côtés qui restent vérifiées dans les déplacements

- Phase 11 / par groupes de 2 / exécution de la tâche

- Phase 12 / collective / synthèse sur le carré et sur l'ensemble des quadrilatères Se servir du vidéoprojecteur et faire exécuter les déplacements par différents élèves. Vérifier la justesse des propriétés dans la quatrième colonne du tableau.

Dans un cabri-carré deux sommets sont attrapables et déplaçables librement, deux sommets sont seulement entraînables.
Un carré est à la fois un rectangle et un losange.


Fermer

Synthèse sur les quadrilatères: Matériel

Matériel nécessaire pour chaque groupe d'élèves :

  • un ordinateur avec le menu simplifié "para2.men"
  • les fichiers "parallelogramme.fig", "losange.fig", "rectangle.fig" et "carre.fig" sur chaque ordinateur.
  • un tableau par élève (cf. fichiers annexes)

Matériel nécessaire pour l'enseignant

  • si possible un vidéoprojecteur pour corriger.


Fermer

Synthèse sur les quadrilatères: Objectifs

Dans cette séance
- redonner les propriétés des quadrilatères particuliers concernant l'isométrie et la perpendicularité des côtés, les propriétés des diagonales
- faire "voir" la hiérarchie des quadrilatères
- approfondir la réflexion sur la nature des objets créés dans Cabri.
Fermer
2024 MAGESI - C.Rolet