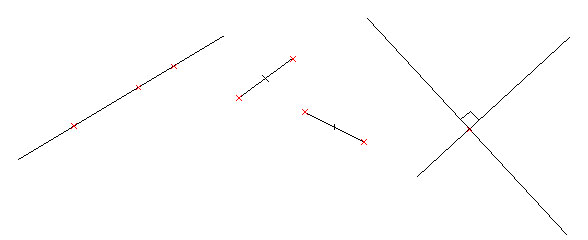
Objets de base (de la géométrie plane)

Dans cette catégorie se trouvent le point, le segment, la droite, l'angle.

Ils ne figurent dans les textes officiels que comme arguments des relations à étudier. Il est par ailleurs demandé que ces mots soient utilisés à bon escient.

Relations de base

Elles sont premières (mathématiquement et psychologiquement), montrées et non définies, et portent sur des objets de base.
Dans cette catégorie se trouvent l'alignement, l'égalité de longueurs (l'isométrie) et la perpendicularité.

Les élèves doivent avoir des connaissances à leur propos, leur permettant d'utiliser des instruments divers pour reconnaître, décrire et construire des objets liés par ces relations, en particulier dans des configurations classiques de figures planes.

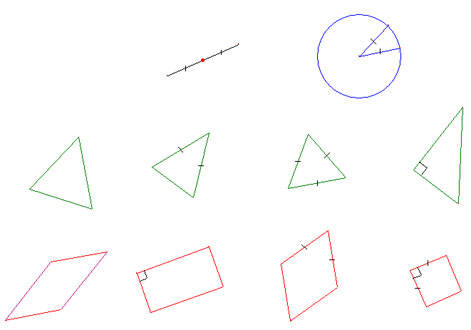
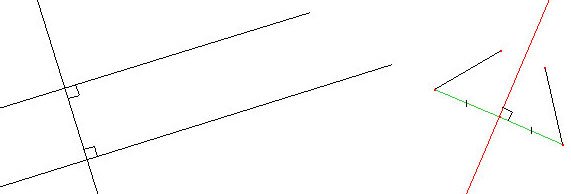
Objets construits

Ce sont les objets définis à partir des objets de base et des relations de base. Ce sont au cycle 3 de l'école élémentaire le milieu d'un segment, le cercle et ce que les textes officiels appellent les figures planes particulières.

Le milieu d'un segment est le point qui partage ce segment en deux segments de même longueur. Le cercle est (théoriquement, dans le savoir à enseigner) l'ensemble des points situés à une distance donnée d'un point donné : en effet il est abordé à l'école élémentaire en liaison avec l'utilisation du compas ; mais les conceptions des élèves peuvent faire penser que pour eux le cercle est parfois un objet de base (le cercle est vu comme "un rond").
Toutes les figures planes dont l'approche est demandée dans les textes officiels peuvent se décrire et se construire à partir de segments et des relations de base ci-dessus. Dans les invariants opératoires du concept de carré il y a nécessairement des invariants liés aux concepts de segment, de perpendicularité et d'isométrie.

Relations construites

Dans cette catégorie se trouvent le parallélisme et la symétrie axiale.

Le parallélisme est une relation que l'on peut choisir de présenter aux élèves comme une relation construite. Dans un premier temps et en ne se fiant qu'au contrôle perceptif simple, la relation peut être vue comme étant de base, et les droites parallèles être reconnues ou tracées à vue. Mais dans un deuxième temps, le seul moyen de reconnaître avec un contrôle instrumenté "correct" et de construire deux droites parallèles est de les voir comme perpendiculaires à la même droite ou à une distance constante l'une de l'autre. Le parallélisme est alors construit à partir de la perpendicularité et/ou de l'isométrie.
La symétrie axiale est de même, au-delà de la première perception globale qui peut la faire voir comme une relation de base, construite avec les relations d'isométrie et de perpendicularité.

Le savoir à enseigner est structuré en l'envisageant comme ensemble de concepts au sens de Vergnaud (Vergnaud 1990).

" Un concept est un triplet de trois ensembles C= (S, I, S)
S : ensemble des situations qui donnent sens au concept (la référence)
I : ensemble des invariants sur lesquels repose l'opérationalité des schèmes (le signifié)
S : ensemble des formes langagières et non langagières qui permettent de représenter symboliquement le concept, ses propriétés, les situations et les procédures de traitement (le signifiant) "

Cette définition est faite, au dire de son auteur, pour comprendre les filiations et les ruptures dans le développement et l'apprentissage de compétences complexes. Le concept est ici lié au sens qu'il peut avoir pour un sujet (générique) dans une vision cognitiviste¹.

Les invariants opératoires correspondent aux connaissances contenues dans les schèmes d'un sujet c'est-à-dire dans l'organisation invariante de sa conduite pour une classe de situations données. Ces invariants opératoires sont de 3 types : des invariants de type proposition (théorèmes-en-acte), des invariants de type fonction propositionnelle (concepts-en-acte ou catégories-en-acte : propriétés ou relations), et des invariants de type argument intervenant dans les deux précédents. Ces connaissances sont plus ou moins conscientisées ou automatisées, les schèmes sont disponibles ou en construction selon les sujets.

En géométrie, les signifiants prendront les formes de dessins, de symboles, d'énoncés en langue naturelle et/ou en langue formelle (lien avec l'utilisation de différents registres au sens de Duval (Duval 1995).

Enfin, Vergnaud va plus loin en considérant qu'un concept ne vit pas seul, mais est pris dans un champ conceptuel, ensemble des situations et ensemble des concepts et théorèmes qui permettent d'analyser les situations qui lui sont associées.

¹ perspective d'étude de la connaissance et de ses processus d'acquisition